The Saving Approach | Multiplier |CBCS

The Saving/Investment Approach to Equilibrium

Because aggregate income must be saved or spent, by definition, Y =C + S, which is an identity.

The equilibrium condition is Y = C + I, but this is not an identity because it does not hold when we are out of equilibrium. By substituting C + S for Y in the equilibrium condition, we can write:

C + S = C + I

Because we can subtract C from both sides of this equation, we are left with:

S = I

Thus, only when planned investment equals saving will there be equilibrium.

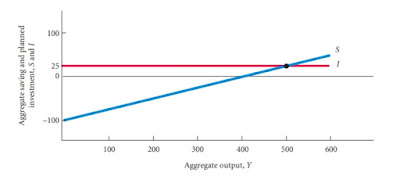
Notice that S = I at one and only one level of aggregate output, Y = 500. At Y = 500, C = 475 and

 I = 25. In other words, Y = C + I; therefore, equilibrium exists.

The S = I Approach to Equilibrium

Aggregate output is equal to planned aggregate expenditure only when saving equals planned investment (S = I). Saving and planned investment are equal at Y = 500.

Adjustment to Equilibrium

We will learned how firms might react to disequilibrium.

Let us consider the actions firms might take when planned aggregate expenditure exceeds aggregate output (income).

We already know the only way firms can sell more than they produce is by selling some inventory. This means that when planned aggregate expenditure exceeds aggregate output,unplanned inventory reductions have occurred. It seems reasonable to assume that firms will respond to unplanned inventory reductions by increasing output. If firms increase output,income must also increase. (Output and income are two ways of measuring the same thing.)

As GM builds more cars, it hires more workers, buys more steel, uses more electricity, and so on. These purchases by GM represent income for the producers of labour, steel, electricity, and so on. When firms try to keep their inventories intact by increasing production, this will generate more income in the economy as a whole. This will lead to more consumption. Remember, when income rises, so does consumption. The adjustment process will continue as long as output (income) is below planned aggregate expenditure. If firms react to unplanned inventory reductions by increasing output, an economy with planned spending greater than output will adjust to equilibrium, with Y higher than before. If planned spending is less than output, there will be unplanned increases in inventories.

In this case, firms will respond by reducing output. As output falls, income falls, consumption falls, and so on, until equilibrium is restored, with Y lower than before.

Read :  Aggregate Expenditure and Equilibrium Output | MacroEconomics

As Figure shows, at any level of output above Y = 500, such as Y = 800, output will fall until it reaches equilibrium at Y = 500, and at any level of output below Y = 500, such as Y = 200,output will rise until it reaches equilibrium at Y = 500.

The Multiplier

The multiplier is defined as the ratio of the change in the equilibrium level of output to a change in some exogenous variable.

 An exogenous variable is a variable that is assumed not to depend on the state of the economy—that is, a variable is exogenous if it does not change in response to changes in the economy.

With planned investment exogenous, we can ask how much the equilibrium level of output changes when planned investment changes.

Consider a sustained increase in planned investment of 25—that is, suppose I increases from 25 to 50 and stays at 50. If equilibrium existed at I = 25, an increase in planned investment of 25 will cause a disequilibrium, with planned aggregate expenditure>aggregate output by 25. Firms immediately see unplanned reductions in their inventories. As a result, firms begin to increase output.

If planned investment (I) goes up by 25 initially and is sustained at this higher level, an increase of output of 25 will not restore equilibrium because it generates even more consumption spending (C). People buy more consumer goods. There are unplanned reductions of inventories of basic consumption items. The cycle starts all over again.

Assume that the economy is in equilibrium at point A, where equilibrium output is 500. The increase in I of 25 shifts the AE = C + I curve up by 25 because I is higher by 25 at every level of income. The new equilibrium occurs at point B, where the equilibrium level of output is 600. Like point A, point B is on the 45° line and is an equilibrium value. Output (Y) has increased by 100 (600 - 500), or four times the initial increase in planned investment of 25, between point A and point B. The multiplier in this example is 4. At point B, aggregate spending is also higher by 100. If 25 of this additional 100 is investment (I), as we know it is, the remaining 75 is added consumption (C). From point A to point B then, ΔY = 100, ΔI = 25, and ΔC = 75.

The size of the multiplier depends on the slope of the planned aggregate expenditure line. The steeper the slope of this line, the greater the change in output for a given change in investment. When planned investment is fixed, as in our example, the slope of the AE = C + I line is just the marginal propensity to consume (ΔC/ΔY). The greater the MPC, the greater the multiplier.

The Multiplier Equation

Assume that the market is in equilibrium at an income level of Y = 500. Now suppose planned investment (I)—thus, planned aggregate expenditure (AE)—increases and remains higher by 25. Planned aggregate expenditure is greater than output, there is an unplanned inventory reduction, and firms respond by increasing output (income) (Y). This leads to a second round of increases, and so on.

What will restore equilibrium? Planned aggregate expenditure (AE = C + I) is not equal to aggregate output (Y) unless S = I; the leakage of saving must exactly match the injection of planned investment spending for the economy to be in equilibrium.As income rises, consumption rises and so does saving. Our S = I approach to equilibrium leads us to conclude that equilibrium will be restored only when saving has increased by exactly the amount of the initial increase in I. Otherwise, I will continue to be greater than S and C + I will continue to be greater than Y.

It is possible to figure how much Y must increase in response to the additional planned investment before equilibrium will be restored. Y will rise, pulling S up with it until the change in saving is exactly equal to the change in planned investment—that is, until S is again equal to I at its new higher level. Because added saving is a fraction of added income (the MPS), the increase in income required to restore equilibrium must be a multiple of the increase in planned investment.

Recall that the marginal propensity to save (MPS) is the fraction of a change in income that is saved. It is defined as the change in S (ΔS) over the change in income (ΔY):

Because ΔS must be equal to ΔI for equilibrium to be restored, we can substitute ΔI for ΔS and

solve:

As you can see, the change in equilibrium income (ΔY) is equal to the initial change in

planned investment (ΔI) times 1/MPS. The multiplier is 1/MPS:

Because MPS + MPC = 1, MPS = 1 - MPC. It follows that the multiplier is equal to

In our example, the MPC is .75; so the MPS must equal 1 - .75, or .25. Thus, the multiplier is 1 divided by .25, or 4.

If planned investment falls by a certain amount and is sustained at this lower level, output will fall by a multiple of the reduction in I. As the initial shock is felt and firms cut output, they lay people off. The result: Income, and subsequently consumption, falls.

Feel Free to Contact,

Don't Forget to Subscribe for Updates.

Do Like ,Comment and Share.